- Intro
Il concetto di “Tensegrità”, in inglese “Tensegrity”, deriva dalla combinazione di due parole inglesi: “tensile” e “integrity”, indicando quindi un sistema costituito da elementi in tensione che formano un’unità strutturale in grado di sostenere il loro peso proprio e eventuali sovraccarichi. Esso caratterizza la capacità di un sistema strutturale di stabilizzarsi meccanicamente mediante uno stato di auto-equilibrio indotto da una pre-sollecitazione degli elementi che lo compongono. La definizione di struttura tensegrale è chiarita immediatamente dall’ingegnere-architetto-scienziato-filosofo Richard Buckminster Fuller definendola come «assemblaggio di elementi tesi e compressi in cui gli elementi tesi sono continui e quelli compressi discontinui». Questa definizione esalta implicitamente la leggerezza delle strutture tensegrali: alcuni elementi -puntoni- sollecitati esclusivamente a compressione costituiscono una maglia discontinua, altri, invece, – tiranti – sollecitati esclusivamente a trazione, formano un insieme continuo.
In tal senso, queste strutture risultano essere automaticamente ottimizzate sin dal loro concepimento: gli elementi compressi, presentando problemi di instabilità per carico di punta, devono essere più tozzi, mentre gli elementi tesi possono essere più snelli e sfruttare a pieno le caratteristiche meccaniche del materiale (figura 1 e figura 2).
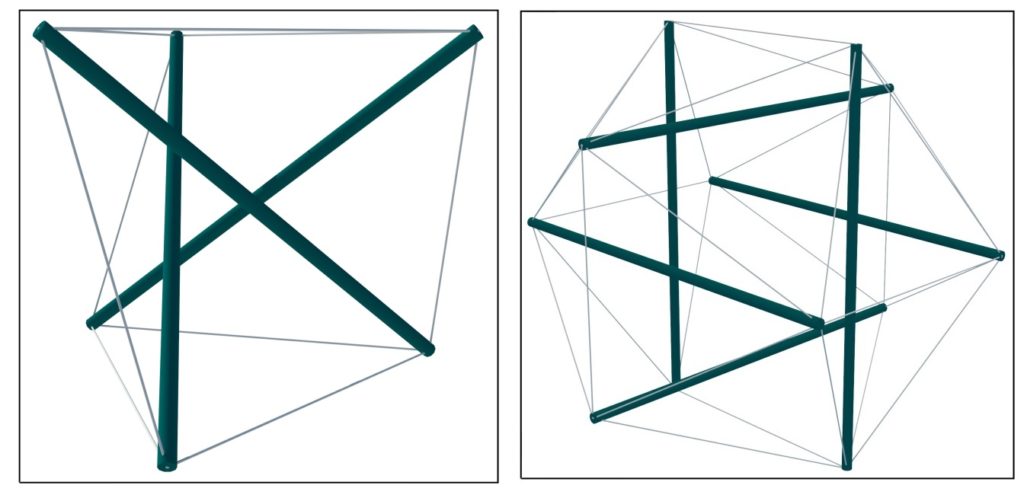
Figura 1 (a sinistra) e Figura 2 (a destra). Esempi di tensegrity: elementi in verde sollecitati a compressione, in grigio quelli sollecitati a trazione.
In generale, quindi, le strutture tensegrali presentano alcune caratteristiche fondamentali che ne esaltano le loro prestazioni strutturali e la loro perfetta rispondenza ad alcuni temi dell’architettura.
In primo luogo, possono essere considerate strutture reticolari spaziali costituite da elementi compressi – aste – e elementi pre-tesi – cavi in acciaio – che pertanto, sono caricati soltanto nodalmente e possono essere sollecitati esclusivamente a compressione o trazione (non presentano sollecitazioni di momento flettente, taglio e torsione). Il sistema costruttivo di queste tensegrity consente di creare forme estremamente affascinanti, i cui elementi puntoni appaiono sospesi all’interno di una maglia continua di tiranti, quasi evanescenti, tanto è che lo scultore Snelson preferisce riferirsi a queste strutture con il termine di “floating compression”, ovvero compressione fluttuante. Sono generalmente strutture formate da geometrie estremamente semplici e regolari, tetraedri, esaedri, ottaedri che conferiscono rigidezza all’intero sistema: questa regolarità consente la modularità e la possibilità di assemblare a secco queste strutture per moduli prefabbricati. Svolge un ruolo fondamentale per il meccanismo strutturale e per la stabilità del sistema lo stato di pre-stress degli elementi, che conferisce inoltre una riserva di energia elastica che da un lato ne aumenta la duttilità in seguito a sovraccarichi eccezionali, dall’altro consente a queste strutture di divenire dispiegabili, aumentando la loro dimensione complessiva e adattandosi a geometrie differenti.
Le tensegrity si prestano, quindi, in maniera eccellente alla possibilità di coprire grandi luci, lavorando in regime estensionale e non flessionale e consentono di sagomare forme geometriche complesse, che possono, non solo rispondere a requisiti statici e funzionali, ma anche architettonici, aderendo perfettamente a temi tipici dell’architettura, come quello della copertura e del ponte.
Inoltre le strutture tensegrali, rispetto a tipologie strutturali affini che adempiono alle stesse funzioni, possono essere sicuramente considerate come sistemi altamente ottimizzati con buone prestazioni strutturali: garantiscono generalmente un minore utilizzo di materiale, ottimizzandone la sua disposizione e mirano a un’ottimizzazione del rapporto rigidezza-peso: la resistenza meccanica complessiva è di gran lunga superiore alla resistenza dei singoli elementi, pur non sacrificando la leggerezza intrinseca di tutte le aste e i tiranti.
Le tensegrity, quindi, sono delle strutture non rigide, flessibili, configurate secondo una precisa forma e vincolate a estremità fisse, in grado di autosostenersi, di rispondere a una specifica condizione di carico e di coprire determinate luci. Come sostenuto precedentemente, trasmettono i carichi esclusivamente in regime estensionale, con sollecitazioni normali semplici, ovvero compressione e trazione, mirando, in un certo senso, alla massimizzazione del tasso di lavoro di tutte le fibre del materiale. Invece, le strutture tradizionali, per esempio quelle intelaiate in cemento armato, per edifici, hanno elementi soggetti a un regime flessionale: le travi e i pilastri. Tali elementi sono sicuramente funzionali a esigenze di carattere architettonico, ma dal punto di vista strettamente strutturale risulta implicito che non tendano all’optimum ingegneristico: tutte le sezioni sono generalmente parzializzate e alcune fibre lavorano a trazione, altre a compressione. Le tensegrity, pertanto, possono essere considerate, a pieno titolo, delle strutture resistenti per forma, la cui genesi costituisce, nel senso più ampio del termine, un processo creativo, dal punto di vista strutturale, architettonico e tecnologico. La forma architettonica denuncia visivamente lo schema strutturale che ne è alla base: si manifesta con chiarezza la sincerità strutturale dell’opera, in cui appare evidente che questa non sia solo il risultato di criteri esclusivamente estetici o architettonici ma che sia anche perfettamente rispondente alle leggi della statica, tendendo sicuramente all’ottimo strutturale nella minimizzazione dell’utilizzo del materiale e nella massimizzazione della sua rigidezza per determinate condizioni di carico e di vincolo. Nonostante alcune problematiche legate ad esempio alla pre-tensione dei tiranti di questi sistemi, le strutture tensegrali rappresentano quindi una soluzione strutturale per problematiche sopra citate, ma il loro impiego risulta ancora piuttosto limitato, poiché i progettisti, come sostiene il celebre ingegnere-architetto Pier Luigi Nervi «non sono – ancora – abituati a ragionare per forma».
- Design optimization
Per quanto detto, quindi, tali strutture, presentano un duplice livello gerarchico di ottimizzazione: in primo luogo, la forma che assumono nello spazio rappresenta la configurazione ottimale in funzione di determinate condizioni di vincolo e di carico; in secondo luogo, gli elementi, a seconda che siano sollecitati a compressione o trazione, hanno sezioni differenti: per i puntoni possono insorgere problemi di instabilità per carico di punta e pertanto sono generalmente più tozzi, al fine di collassare per l’attingimento della tensione di snervamento del materiale e non della tensione critica euleriana, i tiranti, invece risultano essere più snelli, non avendo tali problematiche.
Si intravede pertanto, nelle strutture ispirate alla natura e ai tessuti biologici alcuni principi di design optimization, sia nel superamento del dualismo, soltanto apparente, tra forma architettonica e struttura, sia nell’ottimizzazione dimensionale – sizing optimization – degli elementi che le costituiscono.
Il concetto di ottimizzazione strutturale, sebbene perfettamente assorbito dalla natura, non è di certo nuovo nel campo delle strutture e dell’architettura: sin dall’epoca medievale, l’architettura gotica mostra sicuramente una rivoluzione epocale dei sistemi strutturali: si passa dalla struttura lineare e continua delle murature delle basiliche romaniche a quella puntuale dell’architettura gotica, in cui gli elementi dell’architettura sono elementi strutturali e risultano strettamente necessari dal punto di vista statico. Nel corso del tempo l’architettura gotica perfeziona questo sistema di pilastri, archi ogivali, archi rampanti e contrafforti che consentono di “seguire” il percorso dei carichi denunciando in maniera eclatante la gerarchia degli elementi, quelli strutturali portanti e quelli decorativi, portati.
Una vera e propria rivoluzione nella tecnica del costruire è stata sicuramente quella adottata da Filippo Brunelleschi, le cui intuizioni nel campo dell’ottimizzazione strutturale, sono perfettamente esplicate nell’esempio della Cupola di Santa Maria del Fiore, a Firenze. Nel corso dei secoli, a partire dal rinascimento, l’evoluzione delle tecniche costruttive e la nascita della scienza delle costruzioni, come disciplina autonoma, ha sempre più spinto i progettisti a orientarsi verso soluzioni strutturali che fossero ottimali per determinate tipologie e schemi statici. In realtà però, senza spingersi troppo lontano, la natura fornisce già modelli che sono il perfetto esempio di ottimizzazione strutturale e di strutture gerarchiche:
volete sapere dove ho trovato la mia ispirazione? In un albero; l'albero sostiene i grossi rami, questi i rami più piccoli e i rametti sostengono le foglie. E ogni singola parte cresce armoniosa, magnifica.
affermava uno dei maggiori esponenti dell’architettura moderna, Antonio Gaudì. Dopo aver studiato la meccanica di strutture biologiche, l’architetto spagnolo, ritiene fondamentale realizzare nelle sue opere una perfetta corrispondenza tra la forma e la struttura portante, così come la natura spontaneamente “ottimizza” la sua forma e la sua geometria, in funzione dei carichi da sopportare. In tal senso, la procedura di ottimizzazione ha lo scopo di rendere la struttura quanto più leggera e resistente possibile, individuando la migliore disposizione di materiale, evitandone l’impiego dove non necessario o dove il tasso di lavoro si presenta molto basso, senza sacrificare la resistenza alle sollecitazioni richiesta. L’architettura di Gaudì costituisce sicuramente un’opera estremamente singolare, in cui assumono un ruolo assolutamente di primo livello sia gli elementi costruttivi, che quelli decorativi che vengono entrambi modellati in base al flusso delle forze che li attraversano, assumendo forme ottimizzate in funzione dei carichi e delle condizioni di vincolo. Egli opera all’interno di un universo formale proprio, i cui riferimenti non sono propri dell’architettura ma della natura e si traducono nella sua opera in forme organiche “bio-inspired”. Nella stessa ottica, qualche decina di anni dopo, è possibile inquadrare lo studio delle strutture tensintegre da parte di Fuller, come strutture ispirate alla natura: queste sono presenti, ad esempio, alla micro-scala dei filamenti del citoscheletro delle cellule, e potrebbero essere riprodotte con maggiore consapevolezza, nei loro principi di funzionamento che tendono perfettamente all’ottimizzazione strutturale, alla scala più grande dell’architettura. In questo senso, le forme della natura, esempi di bellezza, armonia e funzionalità non possono che essere il risultato di un processo di ottimizzazione – non soltanto strutturale – e non sono mai il risultato di processi casuali o spontanei.
Allo stesso modo, Mies Van de Rohe, non intende la sua opera architettonica nell’esasperata ricerca di una forma estremamente complessa e particolarmente entusiasmante dal punto di vista estetico, ma piuttosto si concentra sul processo per il concepimento della forma:
La forma è davvero uno scopo? Non è piuttosto il risultato del processo del dare forma? Non è il processo essenziale? Una piccola modifica delle condizioni non ha come conseguenza un altro risultato? Un'altra forma? Io non mi oppongo alla forma, ma soltanto alla forma come scopo. Lo faccio sulla base di una serie di esperienze e di convinzioni da queste derivate. La forma come scopo porta sempre al formalismo.
La perfetta trasposizione della sua poetica si ha in molte opere di Mies: in particolare si potrebbe citare, in riferimento alle affermazioni precedenti, il celebre e noto Padiglione di Barcellona e la Crown Hall di Chicago. Il Padiglione di Barcellona, ad esempio, è caratterizzato da una copertura piana, il cui interno è costituito da un graticcio con maglia e passi differenti, in funzione della distribuzione delle sollecitazioni interne e da setti e pilastri estremamente snelli disposti secondo rapporti aurei: rappresenta quindi una perfetta applicazione di ottimizzazione strutturale al fine di ottenere un disegno in pianta e in prospetto con pochi tratti ed essenziale.
Sulla stessa linea, seppur con leggere differenze, si colloca, ovviamente, il pensiero di uno dei maestri dell’architettura del ‘900, Pier Luigi Nervi. Come è noto, la filosofia progettuale di Nervi è fondata su una stretta corrispondenza tra forma e struttura, che non sono altro che aspetti solo apparentemente duali: «l’ubbidienza alle leggi della statica è di per sé garanzia di riuscita estetica». Pertanto ogni opera che rispetti in maniera ossequiosa il principio dell’ottima efficienza e denunci la sua struttura in maniera sincera può ritenersi ampiamente esteticamente soddisfacente. Secondo questa visione, le strutture tensintegre, in quanto direttamente generate dalla natura, risultano quasi automaticamente altamente ottimizzate e potrebbero essere prese in considerazione, con delle opportune modifiche e correzioni, come una nuova risposta a problematiche strutturali di grandi luci. Come detto, gli elementi di queste strutture presentano due dimensioni differenti in funzione del tipo di sollecitazione: quelli sollecitati a compressione hanno sezioni maggiori, quelli sollecitati a trazione sezioni molto più piccole.
- Galilei’s Design Optimization
In tal senso, si potrebbe portare alle estreme conseguenze il discorso del duplice livello gerarchico di ottimizzazione di queste strutture, andando a massimizzare la loro prestazione strutturale: esasperando questa sizing optimization degli elementi, si può pensare di dimensionarli non in funzione del tipo di sollecitazione, ma in funzione dell’entità di questa, al fine di sfruttare al massimo il materiale utilizzato. Viene quindi introdotto un ulteriore livello gerarchico di ottimizzazione, in cui per ogni singola fibra, ogni sezione, ogni elemento viene massimizzato il tasso di lavoro del materiale: le dimensioni degli elementi saranno tutte differenti a seconda dell’intensità della sollecitazione agente. Questo criterio di ottimizzazione può essere chiamato Galilei’s Design Optimization, in onore a uno dei primi scienziati che ha affrontato tale problematica, e non è implementato nei software di calcolo, a differenza delle altre ottimizzazioni note in letteratura: l’ottimizzazione dimensionale, quella di forma e quella topologica. Tale tipo di ottimizzazione presenta due principali vantaggi: consente di lasciar “libera” la forma e non è legata al materiale scelto per la realizzazione della struttura.
Il concetto fondamentale è che per ogni fibra, per ogni sezione, per ogni elemento della struttura la tensione sollecitante (σ) è uguale alla tensione di snervamento (σy) del materiale fratto un coefficiente di sicurezza (γs) (1).
Si può pertanto affermare che le variabili di questo problema di ottimizzazione sono le variabili geometriche, ovvero le variabili di design della struttura stessa per uno schema statico noto e per condizioni di carico assegnate, mentre la funzione obiettivo è rappresentata dalla massimizzazione del tasso di lavoro per ogni sezione. Questa procedura di ottimizzazione può essere implementata per lo studio di una copertura su grande luce, che sia particolarmente snella e poco impattante rispetto al contesto: queste caratteristiche determinano che tale strategia di design possa rappresentare una possibile soluzione alla problematica di conservazione di scavi archeologici all’aperto, che devono essere necessariamente protetti. Il progetto di una copertura su preesistenze archeologiche non è mai banale, ma deve rispondere a diverse istanze contemporaneamente: istanze funzionali e di protezione, istanze architettoniche-compositive e istanze strutturali. La necessità di tutelare e valorizzare gli scavi archeologici implica la realizzazione di una struttura di protezione che abbia il minimo impatto sul contesto, in termini geometrici e in termini di accostamento materico con le preesistenze e che superi, inoltre grandi luci senza appoggi intermedi: una soluzione possibile, per le precedenti motivazioni, è rappresentata da una copertura ottimizzata, che si configura come una travatura reticolare spaziale, ispirata nella sua geometria e nel suo modello di calcolo alle strutture tensegrali. Prima di studiare l’ottimizzazione strutturale di una forma complessa e articolata, quale quella di una travatura ottimizzata o di una copertura, si devono necessariamente affrontare problemi gerarchicamente più semplici. In primo luogo è necessario porsi un problema di ottimizzazione piuttosto semplice, noto in letteratura come “Problema di Galilei”, posto nel trattato di Galilei del 1638 “Discorsi e dimostrazioni matematiche intorno a due nuove scienze attenenti alla meccanica e i movimenti locali”.
Si consideri una trave isostatica a mensola, con carico concentrato applicato all’estremità, a sezione rettangolare. Si ipotizzi di poter variare l’altezza della trave, dipendentemente con l’ascissa longitudinale della stessa, supponendo di aver fissato la base (figura 3).
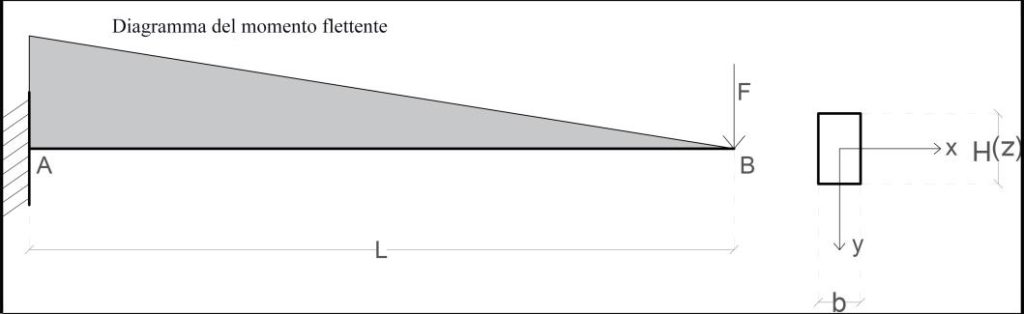
Figura 3. Trave a mensola con carico concentrato all’estremità e sezione rettangolare.
Si intende quindi ottimizzare la trave, in funzione delle condizioni di vincolo e di carico assegnate, ponendosi come obiettivo l’uniformità del tasso di lavoro della trave per ogni sezione, lasciando libera di variare l’altezza della sezione, ma mantenendo costante la base. In tal senso, occorre ricercare la funzione che rappresenti, in funzione dell’ascissa z, il profilo longitudinale ottimizzato della trave, tale che per ogni sezione, la tensione massima sia uguale a quella di snervamento del materiale. Le variabili di un problema di questo tipo sono principalmente variabili geometriche, di cui solo una è l’incognita: l’altezza della sezione H(z), che costituisce ovviamente la variabile di design.
Uguagliando, per ogni sezione, la tensione sollecitante, valutata alla tensione di snervamento del materiale decrementata in funzione di un coefficiente di sicurezza, viene determinato il profilo longitudinale ideale della trave isolando la variabile H(z) che rimane dipendente, logicamente, da z, poiché dipendente dal diagramma del momento che varia linearmente con l’ascissa 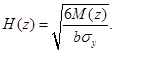(2).
(2)
L’espressione H(z) corrisponde al profilo della trave seguente, risultato dell’ottimizzazione di Galilei (figura 4).
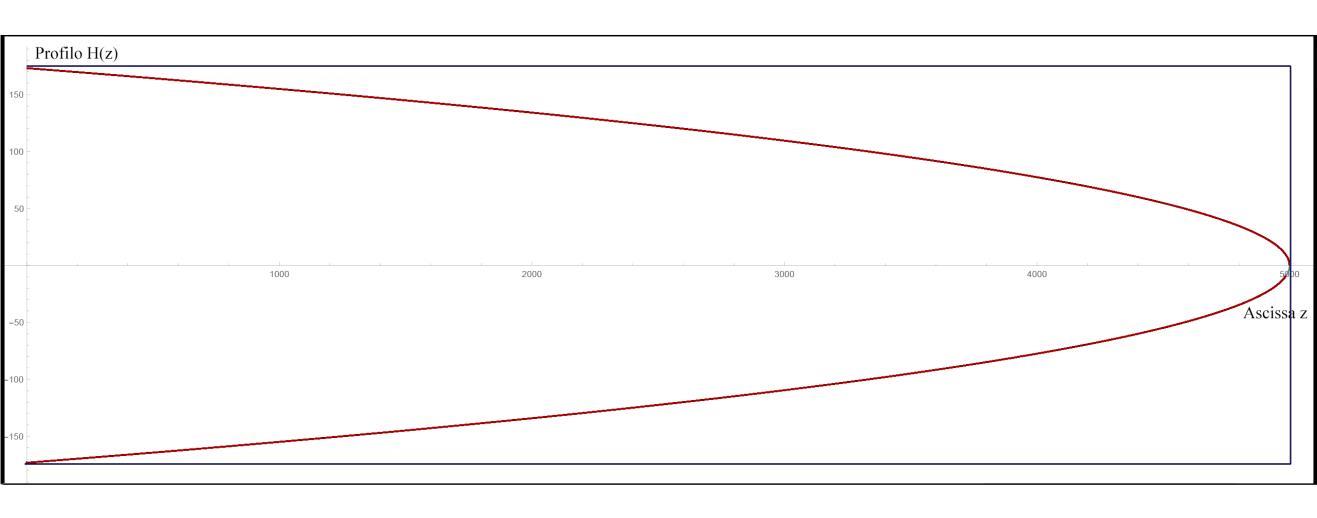
Figura 4. Plot del grafico di H(z): confronto tra un profilo tradizionale non ottimizzato (in blu) e uno ottimizzato (in rosso).
Come precedentemente affermato, la natura assorbe perfettamente i principi della meccanica strutturale, ottimizzando le sezioni dei tessuti biologici in funzione delle condizioni di carico e di vincolo: la parte superiore del becco del tucano presenta una sagoma ottimizzata in funzione di un carico all’estremità che risulta essere qualitativamente simile al plot del grafico precedente (figura 5).
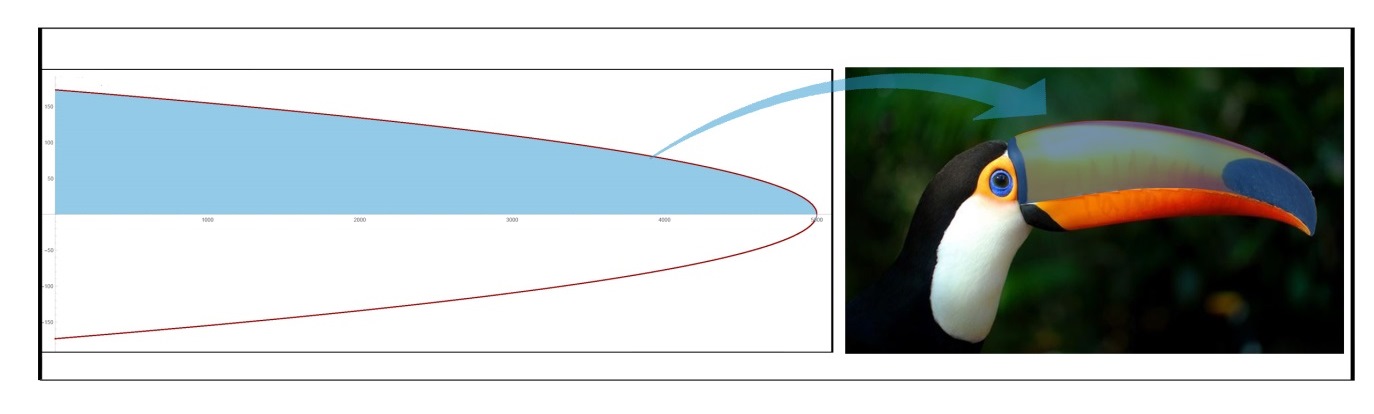
Figura 5. Sagoma del becco del tucano.
Immaginando di voler estendere questa tipologia di ottimizzazione a un’intera struttura di copertura o comunque a una travatura reticolare costituita da aste tubolari, è opportuno porsi il problema di ottimizzare, secondo la stessa logica, di un elemento asta tubolare, a sezione circolare cava sottile, caricato nodalmente. In questo caso, tuttavia, si considera sia il contributo dello sforzo normale, sia quello della flessione, che della torsione e del taglio per il design optimization dell’asta in questione.
La problematica è leggermente più complessa e articolata di quella del caso precedente, in quanto si rimuovono le condizioni di vincolo esterno e si considera un’asta libera generica, sollecitata alla De Saint-Venant (figura 6).
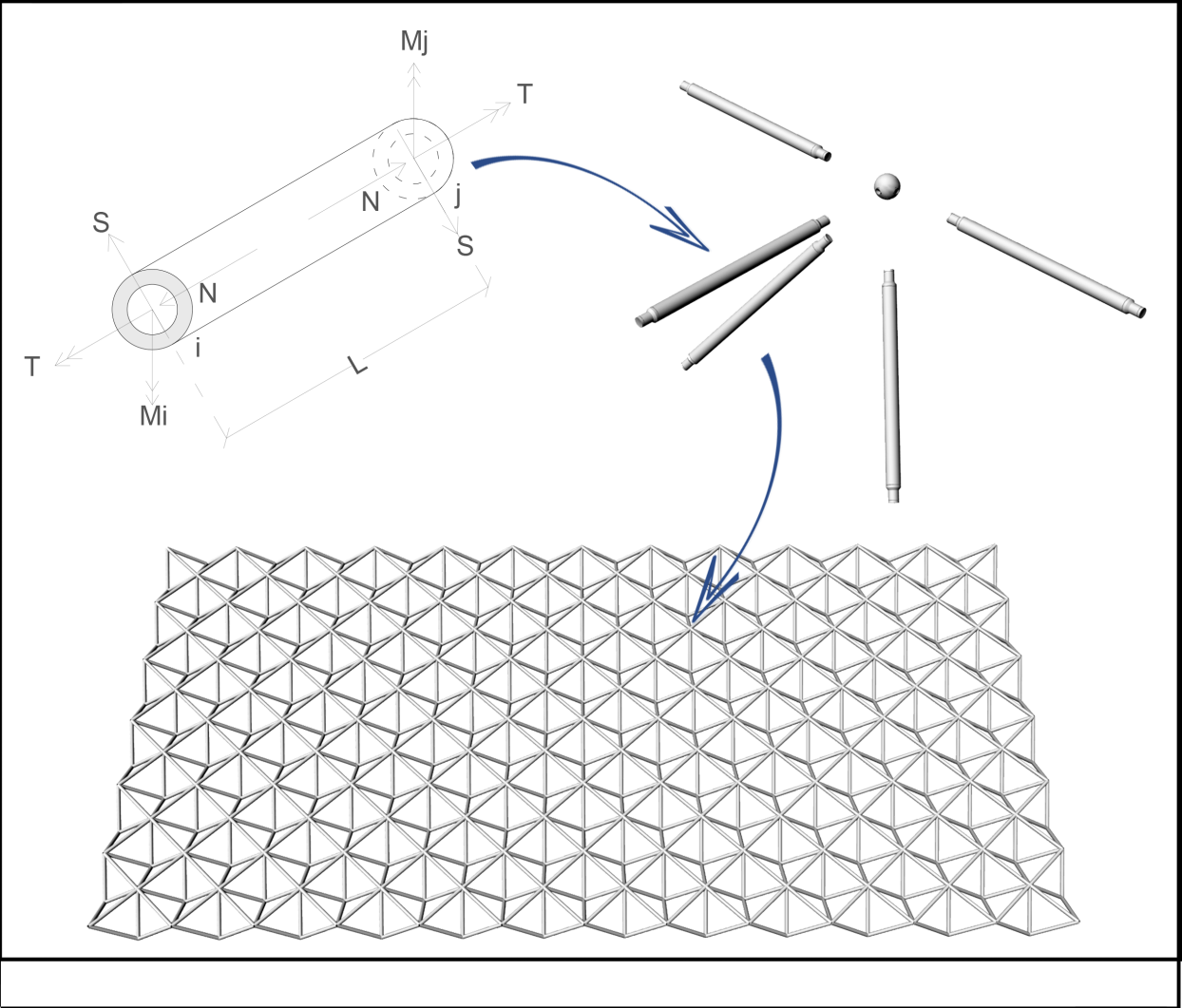
Figura 6. L’elemento asta, il nodo e la copertura.
Anche in questo caso, si intende ottimizzare l’asta, in funzione delle condizioni di vincolo e di carico assegnate, ponendosi come obiettivo l’uniformità del tasso di lavoro della trave per ogni sezione.
Per il caso di sollecitazione più generico possibile, ipotizzando di considerare un materiale duttile, per il criterio di ottimizzazione, verrà considerata la tensione di Hencky-Von Mises.
In tal senso, occorre ricercare, come output della procedura di ottimizzazione non il profilo longitudinale dell’elemento, ma il raggio minimo della sezione che risponde a quelle determinate condizioni di carico. Per questo motivo è necessario ricercare il raggio ottimale tale che la tensione di Hencky-Von Mises (σid) sia uguale alla tensione di snervamento del materiale (σy) rapportata, al solito, a un coefficiente di sicurezza (γs) (3). A differenza del casi precedente, in cui è stata valutata soltanto la flessione, dovendo estendere la trattazione a un’asta non vincolata sollecitata nel modo più generico possibile, oltre alle σ dovute allo sforzo normale e alla flessione, si avranno anche dovute alle sollecitazioni di taglio e torsione.
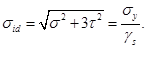(3)
Implementata la procedura di ottimizzazione per l’elemento asta è possibile operare su un’intera copertura per grandi luci, andando a definire il minimo raggio per ogni singolo elemento (figura 7).
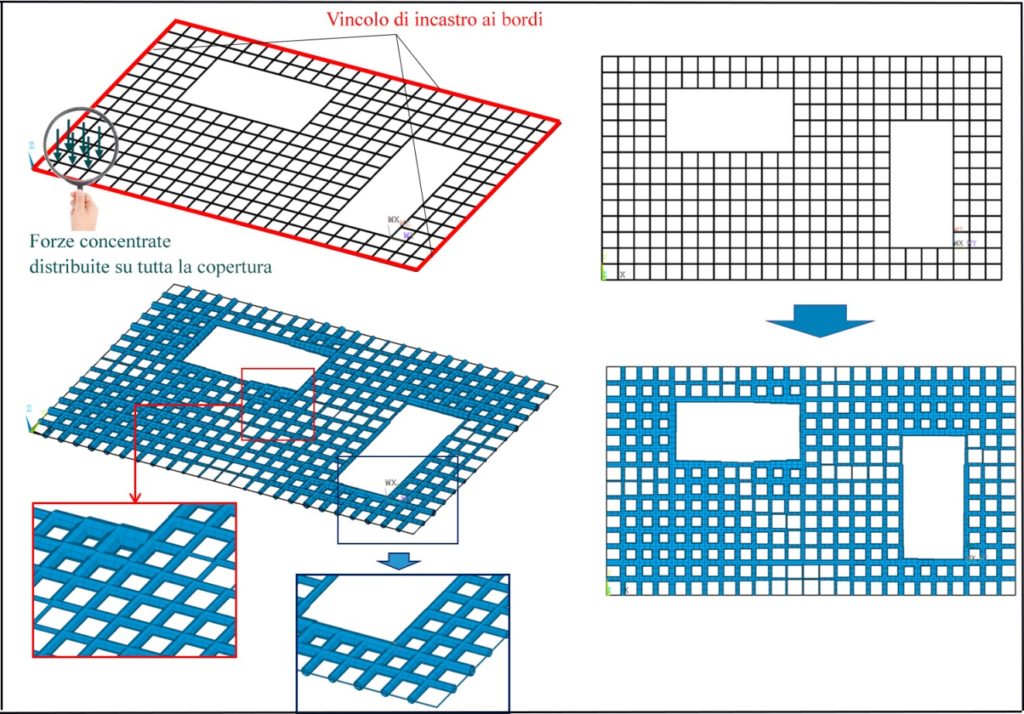
Figura 7. Esempio dell’ottimizzazione di una copertura rettangolare con due fori.
La struttura così modellata presenta, logicamente, sezioni estremamente sottili: risulta infatti “prosciugata” di tutto il materiale – in eccesso – il cui tasso di lavoro è troppo basso e non consente di sfruttare in maniera ottimale la resistenza del materiale. Tutto ciò risulta essere un chiaro vantaggio per la prestazione strutturale: viene minimizzato, in tal modo, il rapporto peso-rigidezza, realizzando una struttura a elevata resistenza e buona leggerezza, costituita da elementi il cui numero e le cui dimensioni sono strettamente necessarie: rimuovendone oppure restringendone uno solo, la struttura collassa. Come sostenuto precedentemente, per le dimensioni minime della struttura, questa tipologia di copertura, può rappresentare una soluzione ottimale per superare grandi luci, senza alcun appoggio intermedio e costituire una protezione per le aree archeologiche, garantendo il minimo impatto con le preesistenze archeologiche. Spesso infatti il progetto di una copertura su ritrovamenti archeologici, testimonianza fondamentale e tangibile di epoche storiche pregresse, costituisce, per gli ingegneri e architetti che adempiono all’incarico, un’opportunità prestigiosa, in virtù della responsabilità di intervenire su una materia, quella archeologica, soggetta a problematiche conservative e di restauro così importanti e “delicate”. Accade quindi, a volte, che il progettista fraintenda l’occasione di una copertura di protezione e tutela di un’area di ritrovamenti archeologici come una possibilità per mostrare il proprio estro creativo eccedendo rispetto al compito meramente tecnico affidatogli, come se fosse quasi obbligato, a causa proprio dell’importanza dell’intervento, a conseguire un risultato non immediato, non banale, che non si limiti alla risposta secca e semplice dell’esigenza tecnica. In tal senso sono numerosi gli interventi, realizzati anche da architetti celebri, estremamente complessi, dalle forme esasperatamente particolari che, seppur esteticamente accattivanti, “annebbiano” l’immagine dello scavo, alterando i rapporti tra i volumi e le strutture emerse, che sono sicuramente le vere protagoniste di un progetto del genere.
- Archeologie
I resti architettonici di natura archeologica si presentano prevalentemente frammentari e lacunosi e per essi è ormai invalsa la definizione di rudere; il rischio di alterare l’immagine quale la Storia ha consegnato all’Oggi sconsiglia interventi restaurativi tesi a “ricomposizioni” o “ricostruzioni” ancorché parziali e la consistenza dei monumenti in “rudere” e la necessità di “conservare” consigliano sempre più frequentemente la realizzazione di coperture a protezione. Il risultato è spesso straniante, considerando che la copertura moderna, articolata secondo moduli spaziali, architettonicamente di forte caratterizzazione, diventa prevalente sui valori architettonici e storici del monumento protetto. Le coperture moderne, per la necessità strutturale di punti di appoggio interferiscono con le strutture antiche e incidono sugli originari calpestii, al di sotto dei quali si celano i segni di precedenti fasi di vita: una sorta di bacino di conservazione archeologica, un ulteriore archivio di dati storici degno di essere preservato, con l’obbligo di limitare nella misura più ampia possibile appoggi a terra o nel sottosuolo.
Ma in linea teorica, al di là anche del campo dell’architettura, supponendo di non voler considerare le vie di mezzo, ci sono due modi per fare una qualsiasi “cosa”: realizzare un qualcosa di estremamente complesso e innovativo o mantenere – non in senso spregiativo – un profilo diverso, mirando all’essenzialità, alla semplicità e alla linearità. «La verità si ritrova sempre nella semplicità, mai nella confusione», sosteneva il celebre fisico del ‘600, Isaac Newton; «Less is more», è la famosissima frase di Mies Van De Rohe. In tal senso,
posta pertanto la stretta correlazione tra restauro e protezione dei siti archeologici ne consegue che i relativi interventi investono generalmente il campo di attività dell’architetto, un architetto però che, seppure particolarmente preparato nello specifico settore di cui si parla, sia capace, con quell’umiltà che in questo caso è sinonimo di alta consapevolezza critica, di utilizzare la sua creatività per conservare ed esaltare, con il suo intervento, l’assoluto protagonismo della preesistenza[1].
Un intervento in aderenza a questi principi, che si proponga sia di tutelare lo scavo e la sua immagine, senza alterarla, sia di consentire la sua conservazione attraverso una completa valorizzazione del sito è quello studiato per la protezione della C.D. “Villa Augustea” ubicata a Somma Vesuviana, in provincia di Napoli, in Italia.
Lo scavo, ancora in corso, della cosiddetta Villa “Augustea” (Figura 8, Figura 9 e Figura 10) a Somma Vesuviana (Napoli) in località Starza della Regina, è diretto dal Prof. Masanori Aoyagi su progetto del Prof. Antonio De Simone, ed è a opera della University of Tokyo, Komaba – Graduate School of Arts and Sciences, su concessione del Ministero dei beni e delle attività culturali e del turismo.
Al progetto, che coinvolge numerosi Istituti di Ricerca e Università giapponesi e europee, partecipano, fornendo apporti fondamentali anche Satoshi Matsuyama, Claudia Angelelli, Girolamo F. De Simone, Akira Matsuda.
L’attuale stadio della ricerca impedisce una dettagliata e definitiva lettura del monumento, anche se è legittima l’ipotesi che esso sia da indentificare in una vasta villa romana, costruita verso la metà del II sec. d. C. e sotterrata, dopo incisivi mutamenti e trasformazioni, da una rovinosa eruzione del Vesuvio del 472 d. C.
Le strutture finora riportate in luce costituiscono l’ingresso monumentale dell’imponente villa.[2]
Figura 8. Foto del vestibolo della “Villa Augustea”.
Figura 9. Foto delle aree absidali della “Villa Augustea”.
Figura 10. Foto della “Villa Augustea” temporaneamente scoperta.
Il punto di partenza dello scavo attualmente in corso, avviato nel 2002, era costituito dall’esplorazione condotta a partire dal 1930 e limitata a circa mq 25, a seguito del casuale rinvenimento di murature antiche, occasionato da lavori agricoli. L’imponenza delle strutture e l’erronea lettura della matrice dell’interro, effettuata da vulcanologi dell'Università di Napoli e ricondotta ai materiali vulcanici del 79 d. C., diedero vigore all’ipotesi che il monumento potesse essere identificato come la villa in cui era morto l’Imperatore Augusto, sulla scorta delle testimonianze di Svetonio e Tacito, che ricordano con dovizia di particolari la morte di Ottaviano Augusto nella campagna di Nola (apud Nolam) in una dimora di proprietà degli Octavii successivamente trasformata, secondo la testimonianza di Dione Cassio, in luogo di culto in memoria dell'Imperatore. Da tanto deriva il nome di Villa Augustea, conservato in omaggio alla tradizione ma errato alla luce dei risultati delle moderne indagini.
La limitatezza delle risorse disponibili e la partecipazione dell’Italia al secondo conflitto mondiale impedirono la prosecuzione degli scavi e nell’arco di un decennio il saggio fu naturalmente colmato.
I risultati degli scavi a oggi eseguiti, pure nella limitatezza dell'area esplorata a fronte dell'ipotetica articolazione del sito archeologico, sono utili a definire le caratteristiche in una prospettiva di lunga durata di un territorio finora trascurato. Oltre alla villa di Somma, oggetto di indagine, sopravvivono tracce di numerose villae che si sviluppavano a oriente di Napoli lungo la direttrice che conduceva a Nola mostrano la vitalità e la produttività di un territorio ben oltre il limite altrove imposto dalla disastrosa eruzione del 79 d. C.. Le ville nascono come ricche dimore nell'ager nella scia dell'attività di riassetto dell'area colpita dall'eruzione promossa dall'Imperatore Tito e realizzata dai Curatores restituendae Campaniae e quindi sono riconducibili all’assegnazione di estese porzioni di territorio nelle mani di grandi investitori o di personaggi appartenenti al ceto senatorio.
Gli ambienti fino a oggi posti in luce, distribuiti su una superficie di circa mq 2.500, individuano spazi architettonici di notevole qualità e raffinatezza e di particolare ricchezza, quale quella indiziata dalla monumentalità degli spazi e dai materiali usati, difficilmente riscontrabili nelle ville edificate nella regione.
La villa è costruita per terrazze, assecondando il pendio che dal Vesuvio si sviluppa verso la pianura. La natura dei luoghi ha condizionato una costruzione sul livelli differenti che sono raccordati da scale secondo un modello già ben presente nelle ville del I secolo lungo la fascia costiera e che caratterizza le ville fino a tutto il V secolo d. C.
La Villa è composta da diversi nuclei collegati da aree di raccordo, pavimentate in basoli. A oggi è stato posto in luce il nucleo di ingresso monumentale, dove il dominus accoglieva visitatori e clientes, normalmente esclusi dall'accesso alle parti private della dimora.
L’aula centrale è configurata in una grande esedra poligonale con muri articolati in nicchie semicircolari e rettangolari originariamente ornate da statue. A essa si raccordano saloni monumentali, ornati da decorazioni dipinte, trasformati nelle ultime fasi di vita in ambienti e aree destinati alla conservazione dei prodotti agricoli e principalmente del vino.
La Villa di Somma anticipa modelli che sono caratteristici delle ville tardoantiche nelle quali l’ingresso raccorda l’esterno all’interno e rivela lo status del proprietario al visitatore prima che egli entri in casa.
Alla metà circa del IV sec. la Villa subisce incisivi mutamenti con la trasformazione di alcuni ambienti in strutture eminentemente produttive e l'impianto di una vasta cella vinaria sulla terrazza inferiore, dove sono collocati dolia utili a conservare una produzione vinicola stimata in 100.000 litri. I mutamenti comporteranno nel prosieguo dei tempi l'avvio di un processo di spoliazione.
Il monumento così trasformato viene seppellito per circa i 3/4 dell'altezza nel 472 dall’eruzione subpliniana, definita di Pollena e ben nota anche nelle fonti letterarie per lo sgomento suscitato dalle ceneri trasportate fino a Costantinopoli dove ogni anno il 6 novembre ne celebravano il ricordo, come attesta Marcellinus Comes[3].
Ulteriori e meno disastrose eruzioni degli inizi del VI sec. completano l'opera di seppellimento di una struttura ormai già obliterata.
La vastità dell'area indagata e la stretta collaborazione con i vulcanologi ha consentito un notevole accrescimento delle conoscenze relative alla storia del vulcano[4].
Al fine di preservare l’intero complesso che presenta dimensioni variabili dai 30 ai 70 metri, si rende necessario un intervento che riesca a coprire queste grandi luci senza appoggi intermedi e che sia quanto meno invasivo per lo scavo, lasciando inalterata la percezione dei rapporti geometrici, della monumentalità e della magnificenza della villa. In tal senso, al fine di ridurre al minimo la sezione della copertura del sito, per rispondere all’esigenza del minimo impatto sullo scavo, si potrebbe pensare piuttosto che a ottimizzare una struttura portante copertura, modellata come una travatura reticolare spaziale, ad “appendere” l’elemento tecnologico di copertura a delle travi che svolgono funzione portante, liberando la struttura di protezione da oneri strutturali e riducendo ancor di più la sua sezione. La procedura di Galilei quindi, potrebbe essere applicata non a una copertura reticolare, ma direttamente all’armatura in acciaio di queste travi in cemento armato che risulterebbero internamente ottimizzate, in funzione della geometria e delle condizioni di carico.
Sullo spunto della sizing optimization delle strutture tensintegre, implementando l’ottimizzazione di Galilei, anche gli elementi tubolari dell’armatura, assemblati a secco, assumerebbero sezioni differenti in funzione dell’intensità di carico, dando luogo a forme e geometria estremamente e “spontaneamente” organiche (figura 11).
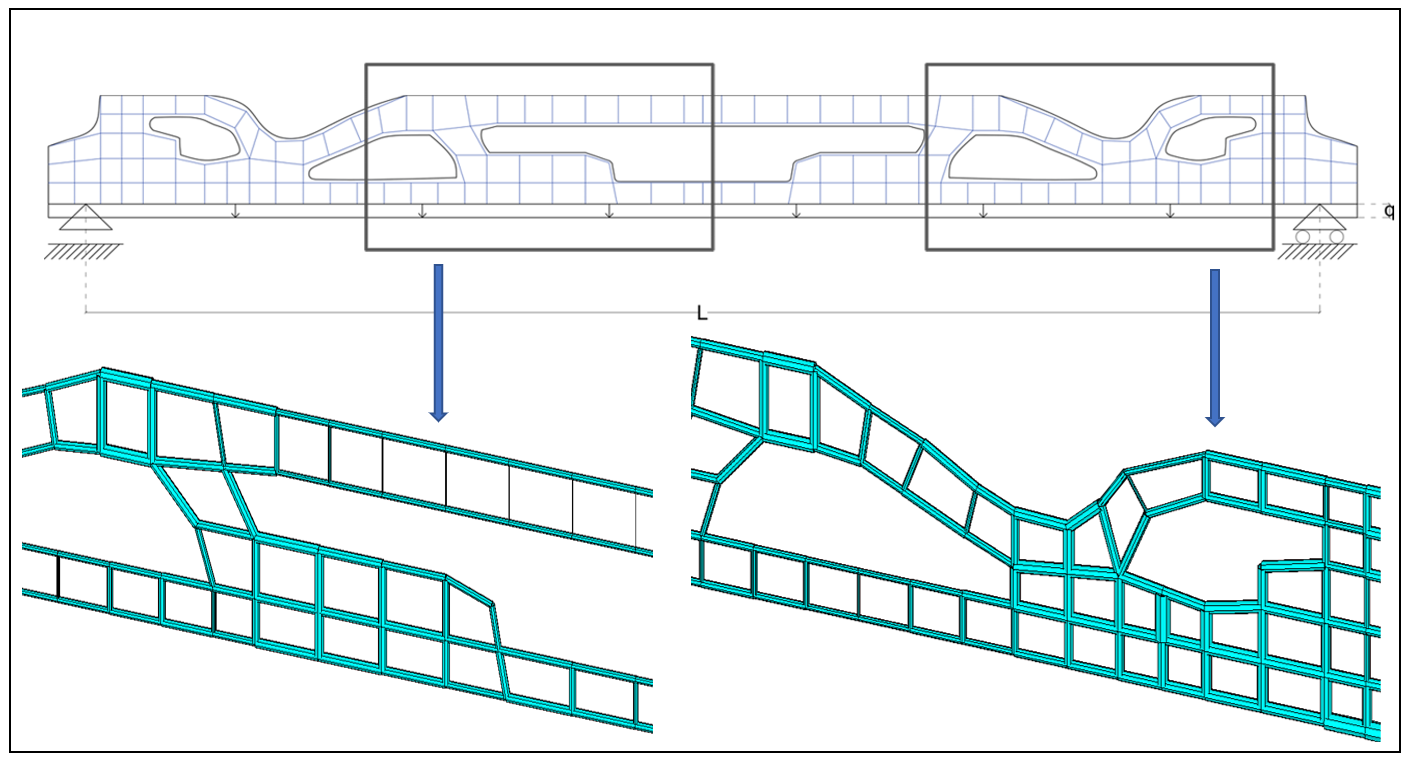
Figura 11. Armatura di una trave ottimizzata.
In conclusione, minimizzando le geometrie degli elementi strutturali, si ottiene l’effetto desiderato di una struttura che assolvesse alle esigenze di carattere tecnico e non interferisse nella sua immagine e nella sua mole con lo scavo (figura 12 e figura 13).
Figura 12. Sezione trasversale dello scavo e della copertura “appesa” alla trave ottimizzata.
Figura 13. Immagini dello scavo della c.d. “Villa Augustea” e della copertura.
[1] La vastissima bibliografia sull’argomento delle coperture in ambito archeologico è disseminata in monografie e articoli e atti di convegno. Una soddisfacente informazione sull’argomento è costituita da S. Rannellucci, Coperture archeologiche, Tipografia del Genio Civile, Roma 2009.
[2] M. Aoyagi, C. Angelelli, S. Matsuyama, Somma Vesuviana, cd. Villa di Augusto: aggiornamenti delle indagini 2009-2010, in «Amoenitas. Rivista Internazionale di Studi Miscellanei sulla Villa Romana Antica», II, 2012, pp. 219-240; M. Aoyagi, C. Angelelli, La cd. Villa di Augusto a Somma Vesuviana (NA). Nuova ipotesi di lettura sulla base delle più recenti ricerche archeologiche, in «Atti della Pontificia Accademia Romana di Archeologia», Serie III. Rendiconti, LXXXV, Anno Accademico 2012-2013, Topografia Vaticana 2013, pp. 171-202; A. De Simone, M. Aoyagi, G. F. De Simone, The Villa “of Augustus” at Somma Vesuviana, Dionysus, and Late Antique Wine Production, in A. Marzano and G. P.R. Métraux (eds.), The roman Villa in the Mediterranean basin (in memory of Ehud Netzer), Cambridge University Press 2018, pp. 141-158.
[3] L’eruzione è datata al 6 novembre 472, durante il consolato di Marciano e Festo: Marcellinus comes, Chronicon, 68, ed. Th. Mommsen, Monumenta Germaniae Historica, Auctores Antiquissimi, XI, Berolini 1894, p. 90.
[4] T. Kaneko, S. Nakada, M. Yoshimoto, T. Fujii, A. Yasuda, M. Yoneda, M. Aoyagi, Determination of burial age of the “Augustus’ villa” (Italy), in «Geochemical Journal», 39, 2005, pp. 573-578; A. Perrotta, C. Scarpato, G. Luongo, M. Aoyagi, Burial of Emperor Augustus’ villa at Somma Vesuviana (Italy) by post-79 AD Vesuvius eruptions and reworked (lahars and stream flow) deposits, in «Journal of Volcanology and Geothermal Research», 158, 2006, pp. 445-466; K. Niihori, M. Nagai, T. Kaneko, T. Fujii, Setsuya Nakada, M. Yoshimoto, A. Yasuda, M. Aoyagi, Detailed Stratigraphical and Geological Characteristics of Volcanic and Epiclastic Deposits Burying a Roman Villa on the Northern Flank of Mt. Vesuvius (Italy), in «Bulletin of the Earthquake Research Institute», University of Tokyo, 82, 2007, pp. 119-178 (http://www.eri.u-tokyo.ac.jp/BERI/pdf/IHO82201.pdf)
