Per commemorare i 500 anni dalla morte di Leonardo da Vinci – che ricorrono nel 2019 – propongo il seguente scritto in forma di intervista virtuale al prof. Giuseppe Maria Pugno (GMP), che ne commemorò i 500 anni dalla nascita[1].

Figura 1. La pagina degli Atti e rassegna tecnica della società degli ingegneri e degli architetti in Torino, del maggio 1952, che riportava la notizia della Commemorazione di Leonardo per i 500 anni dalla nascita da parte del prof. Giuseppe Maria Pugno [1] e introdotta dal sindaco di Torino avvocato Amedeo Peyron.

 

L’intervista, pur di natura virtuale, per via delle due generazioni che separano intervistatore (il sottoscritto, NMP) e intervistato, è tuttavia basata su risposte pienamente reali e date dall’intervistato nei suoi scritti su Leonardo e la “scienza delle costruzioni” ovvero la meccanica dei solidi e delle strutture[2]. L’intervista è quindi confinata all’interno di questa disciplina senza la pretesa di essere completa e volutamente non discute i contributi di Leonardo in altre discipline né all’interno della stessa meccanica, come quella dei fluidi o delle macchine, né tantomeno al di fuori di questa, come la pittura e la scultura. Altri spunti interessanti si ritrovano negli scritti di GMP su Leonardo e le macchine[3], su Leonardo e l’idraulica[4] e sullo sviluppo bicentenario del pensiero scientifico da Dante Alighieri a Leonardo[5], nonché in scritti di altri autori su Leonardo, es. si veda nota[6] e relativi riferimenti. Nell’ultima “botta e risposta”, intervistatore e intervistato si scambieranno i ruoli per gettare uno sguardo sull’eredità di Leonardo per un ricercatore del XXI secolo, fornendo solo pochi esempi[7].

 

NMP: prof. Giuseppe Maria Pugno, sappiamo come il maggior codice Vinciano (quello Atlantico) abbia avuto numerose occasioni di dispersione e fu proprio il materiale disperso e poi ritrovato che dette origine appunto ai Codici minori. Tra questi, quelli che più interessano la Meccanica e in particolare la Scienza delle Costruzioni quali sono?

GMP: sono il Codice Arundelliano, il Codicetto sul volo degli uccelli, i così detti Manoscritti (Man) A e B e, per certi subordinati riguardi, il Codice Trivulziano.

NMP: Leonardo aveva certamente chiara la Statica, per esempio commentando il caso di un carico applicato e sospeso a due fili (si veda disegno originale in Man. A foglio 47 verso) correttamente fa notare come le tensioni nei fili dipendano solo dall’inclinazione degli stessi; secondo lei, aveva anche intuito i teoremi alla base della soluzione delle strutture iperstatiche –come potrebbe diventare il citato esempio nel caso in cui si aggiunga un terzo filo nello stesso piano – ovvero quello dei lavori virtuali (o principio, come definizione del lavoro interno) e quello della minima energia potenziale?

GMP: Ambedue, se non sono enunciati, sono certamente sentiti da Leonardo. Per esempio, Leonardo analizza il caso di due carrucole, come ho schematizzato in Figura 2 (disegno originale in Cod. Atl. 104 v.b.).

 

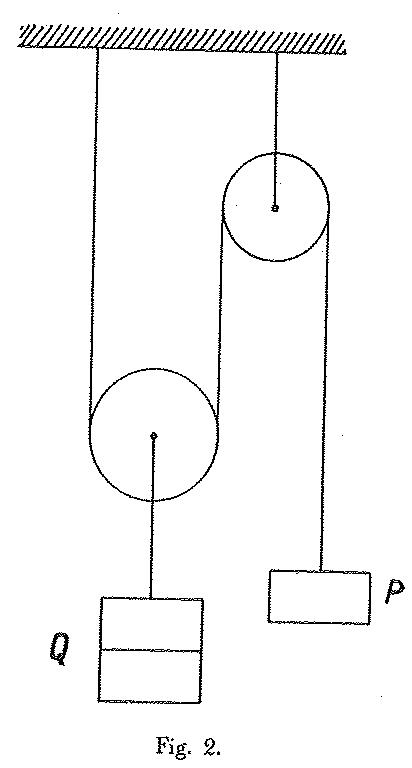
Figura 2: Verso il teorema dei lavori virtuali.

 

Qui troviamo, pur avendolo riconosciuto in un caso particolare (di forze e spostamenti reali), il teorema dei lavori virtuali. Lo stesso Leonardo discute le sue applicazioni, come una specie di tenaglia che io ho denominato “lo schiaccianoci di Leonardo” e schematizzato in Figura 3 (disegno originale in Cod. Atl. foglio 153 recto a)

 

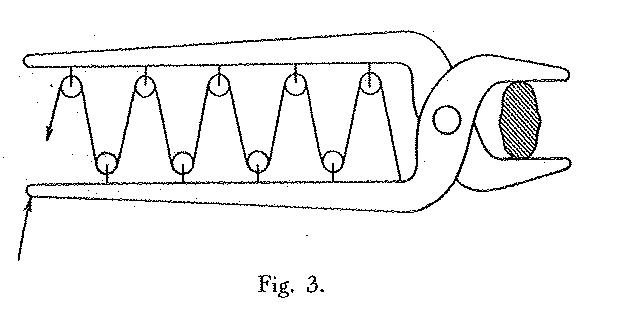
Figura 3: Lo “schiaccianoci di Leonardo”.

 

e la commenta in vari modi (come per esempio «E quella cosa che manco resiste, da minor potenzia fia remossa, a più a lungo moto fia continuata», Cod. Atl. foglio 104 verso b). Circa 100 anni dopo Stevin enunciava la proposizione di Leonardo nella forma seguente: «Ut spatium agentis ad spatium patientis, sic potentia patientis, ad potentiam agentis». Tuttavia bisogna giungere fino a Bernoulli (1717), a Fourier e a Lagrange (1800), per vedere la proposizione di Leonardo espressa nella sua forma più generale e dimostrata nel modo più completo.  

NMP: E tornando al minimo dell’energia?

GMP: Leonardo chiaramente avvertì e scrisse che un corpo sollecitato si porta alla sua naturale situazione (congruente oltre che equilibrata), obbedendo a una precisa condizione di minimo: («Ogni azione naturale – egli scrive – è generata dalla natura nel più brieve modo che trovar si possa», Cod. Atl. foglio 112 verso a). Dovevano però ancora passare circa 350 anni prima dell’enunciato finale nella forma del teorema di Menabrea.

NMP: Per connettere i due mondi di equilibrio e congruenza e quindi risolvere il problema iperstatico, servono però le leggi costitutive: aveva Leonardo intuito la legge di Hooke da quest’ultimo enunciata nel 1678 col suo motto tramite la locuzione latina «Ut tensio sic vis»?

GMP: Leonardo vide chiarissimamente anche questa legge affermando in modo chiaro e netto la proporzionalità tra le forze e le deformazioni da queste prodotte (egli scrive: «Questa molla che ha la forza per 200, sta ferma con peso di 200; ma se tu leverai un minimo di peso, essa molla si drizzerà tanto che si pareggerà con la loro resistenza. E tal proporzione avrà tal moto con la lunghezza della molla quale ha il peso che si tolse col suo rimanente», Cod. Atl. foglio 110 verso b).

NMP: Le forze applicate dall’esterno ai solidi si diffondono nell’interno seguendo certe linee (direttrici) denominate “isostatiche”. Leonardo Aveva intuito le isostatiche?

GMP: Certamente sì, come è evidente quando Leonardo suggerisce «un modo di incatenare le travi che non si pieghino», come ho schematizzato in Figura 4 (disegno originale in Cod. Alt. foglio 9 recto b),

 

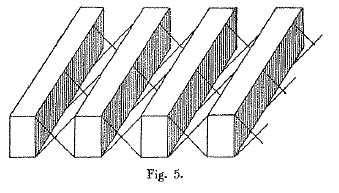
Figura 4: “Un modo di incatenare le travi che non si pieghino”.

 

connessione che forza le travi a lavorare cooperativamente a seguito dell’abbassamento di una di queste.

NMP: Leonardo sembra quindi aver intuito tutte le leggi per la soluzione delle strutture iperstatiche. Aveva anche anticipato, in un qualche modo, l’ipotesi di de Saint Venant?

GMP: Senza dubbio sì. Nello studio dello sforzo normale Leonardo avverte subito che il sistema di attacco non presenta alcuna influenza sulla forma del diagramma delle tensioni a una certa distanza dagli estremi; non soltanto, ma avverte anche che il diagramma presenta una ordinata costante, come schematizzo in Figura 5.

 

 

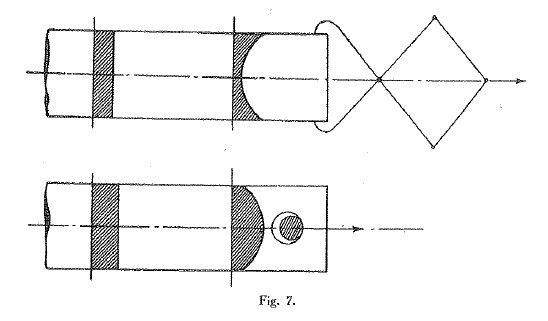
Figura 5: Intuizione del principio di De Saint Venant.

 

Considerando una corda tesa da un carico centrato, cioè spirante secondo l’asse geometrico della corda, scrive: «Ogni parte della grossezza d’essa corda sarà da esso peso ugualmente carica» (Cod. Atl. foglio 153 recto a). Circa 300 anni dopo, Adhémar-Jean-Claude Barré de Saint Venant enunciava il suo principio.

NMP: Leonardo era quindi pronto a progettare strutture reticolari.

GMP: E così fece. Come esempio, si consideri il suo “ponte mobile”, inteso come di rapido montaggio e smontaggio, che ho schematizzato in Figura 6 (si veda disegno originale in Cod. Atl. foglio 312 recto a).

 

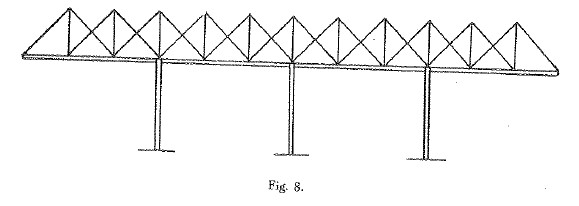
Figura 6: Travata di Leonardo, o di Fink.

 

 

È nella sostanza la travata di “Fink”, dal nome del costruttore americano che la realizzò, circa tre secoli e mezzo dopo. 

NMP: La comprensione dello sforzo normale a compressione e del relativo carico di Eulero e in particolare di come questo sia inversamente proporzionale al quadrato della lunghezza del solido prismatico a sezione costante caricato di punta, doveva essere un problema insormontabile ai tempi di Leonardo, o sbaglio?

GMP: Leonardo ha indubbiamente sentito l’importanza della lunghezza del solido caricato di punta e prende in esame due solidi di eguali sezione rette, ma di lunghezza una decupla dell’altra, come ho schematizzato in Figura 7 (disegno originale in Cod. Atl. foglio 152 recto b).

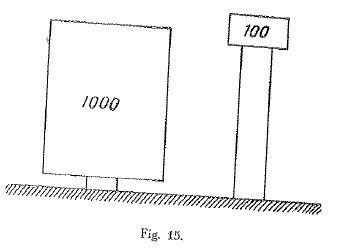
Figura 7: Travaglio di Leonardo sull’influenza della lunghezza del solido sul carico di punta.

 

 

Qui Leonardo indica purtroppo i carichi critici come 100 e 1000 e non il valore corretto per quest’ultimo di 10000.

Più avanti tuttavia dimostra, non solo, di aver compreso l’importanza della lunghezza del solido, ma anche dell’area della sezione trasversale dello stesso. Con un ragionamento involuto invero descrive quanto semplifico in Figura 8,

 

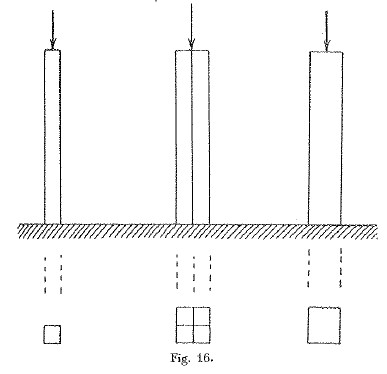
Figura 8: Comprensione di Leonardo dell’influenza dell’area della sezione retta del solido sul carico di punta.

 

deducendo per queste travi come quella singola sopporti un carico critico di P, le quattro disgiunte un carico 4P, mentre se unite tra loro un carico 16P, qui in perfetto accordo con la formula di Eulero.

Su questi argomenti Leonardo ritorna spesso nel Man. A, ai fogli 3 verso 45 verso 46 recto, ed è interessante osservare il tormento delle sue biffature su questo argomento: egli usava segnare o biffare in due modi diversi le proposizioni che egli aveva riconosciute errate e quelle sulle quali egli conservava ancora dei dubbi e sulle quali desiderava ritornare.

NMP: Leonardo si è occupato anche di flessione sia in termini di tensione che di deformazione.

GMP: Nella flessione Leonardo ravvisa erroneamente la proporzionalità diretta tra il momento flettente massimo sopportabile da una trave a sezione rettangolare e ciascuna delle dimensioni della sezione rettangolare. Pur enunciando male la legge tuttavia la sente e la pratica giustamente, riconoscendo la convenienza nel giuntare saldamente due travi per aumentarne la loro altezza complessiva e resistenza, come per esempio seguendo l’accorgimento che ho schematizzato in Figura 9 (si veda disegno originale in Cod. Atl. foglio 344 verso a).

 

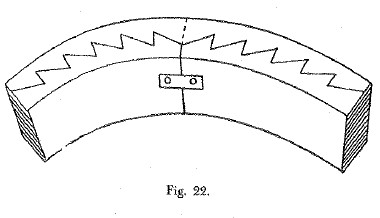
Figura 9: Giunzione di travi per aumentare la resistenza a flessione complessiva.

 

Per quanto riguarda la freccia delle travi inflesse, Leonardo comprende come questa scali col cubo della lunghezza della trave. Considera il caso di travi caricate in mezzeria e di lunghezze via via dimezzate e ricerca i valori delle forze applicate per provocare la stessa freccia, come riporto in Figura 10 e come anche Leonardo (col disegno in Cod. Atl. foglio 211 recto b) lascia chiaramente intendere di pensare.

 

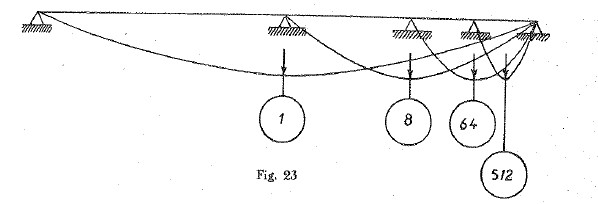
Figura 10: Comprensione della freccia di travi inflesse.

 

Inoltre, si dichiara pronto a dire quale peso P’ è necessario applicare in un dato punto della trave per farle subire la medesima freccia prodotta da un peso noto applicato in mezzeria, superando nella comprensione del Teorema di Betti gli stessi Maxwell e Rayleigh.

NMP: Leonardo mostra di aver compreso anche la torsione, vero?

GMP: Se ne occupa trattando il caso di un fascio di vimini disposti a semplice contatto gli uni con gli altri e lo chiama «fasciculo disarmato». Propone l’armatura a torsione per resistere a un verso solo («fasciculo armato sol per un verso») o a entrambi («fasciculo a un moto per due versi»), come ho schematizzato in Figura 11 (si veda disegno originale in Cod. Atl. foglio 139 recto c).

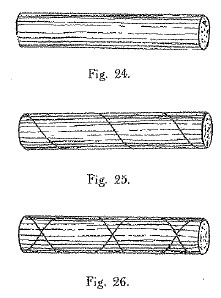
Figura 11: Comprensione delle armature a torsione.

 

 

Mostra quindi chiaramente di aver compreso come le linee isostatiche nella torsione si dispongano a spirale a 45 gradi rispetto all’asse del solido.

NMP: Leonardo tratta anche di sollecitazione composte, per quanto riguarda lo sforzo normale e la flessione e anche di solidi a uniforme resistenza per sforzo normale o flessione, dimostrando di intuirne i fenomeni relativi. E per quanto riguarda la resistenza dei materiali?

GMP: Leonardo, riconoscendo l’importanza della prova di trazione per la caratterizzazione della resistenza dei materiali propone una macchina per la sua realizzazione, come ho schematizzato in Figura 12 (disegno originale in Cod. Atl. foglio 82 recto b)

 

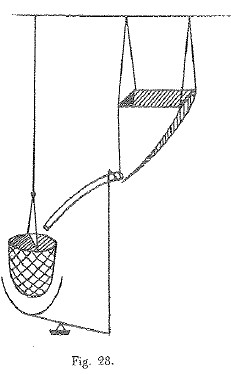
Figura 12: Macchina per prova di trazione.

 

e anche per prove di urti ripetuti come riporto in Figura 13 (disegno originale in Cod. Atl. foglio 21 recto a).

 

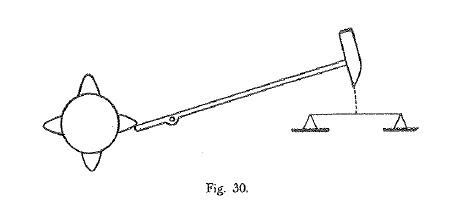
Figura 13: Macchina per prova di urti ripetuti.

 

 

NMP: Nelle impressionanti e note macchine di Leonardo, ne troviamo un certo numero per applicazioni militari e dobbiamo ricordare che Leonardo non era un uomo di guerra, ma di pace, giusto?

GMP: Leonardo giudicava la guerra come una pazzia e scriveva: «E tu uomo, che consideri in questa mia fatica l’opere mirabili della natura, se giudicherai essere cosa nefanda il distruggerla, or pensa essere una nefandissima cosa il tôrre la vita all’uomo; se questa sua composizione» – cioè la vita del corpo – «ti pare di meraviglioso artificio, pensa questa essere nulla rispetto all’anima che in tal architettura abita». Come Dante anche Leonardo giunge alla definizione di Dio come Amore, che per il primo è «Amor che move il sole e l’altre stelle» (Divina Commedia, Par. XXXIII 145) e per il secondo è «Amor qui omnia vincit, et nos cedamus amori» (Cod. Atl. foglio 273 recto a).

NMP: I ricercatori, i politici e l’umanità tutta deve cogliere nel profondo anche questa conquista di Leonardo. E ora un’ultima domanda.

GMP: Questa vorrei farla io a te, che vivi nel XXI secolo. Qual è l’eredità di Leonardo per un ricercatore del tuo tempo?

NMP: Leonardo ha aperto la via anche per quanto riguarda gli studi ispirati alla Natura; le sue macchine volanti ne sono l’esempio più lampante. Oggi abbiamo a disposizione una tecnologia che lui non aveva e che ci consente di osservare i materiali naturali e fabbricarne di bio-ispirati con risoluzione e precisione nanoscopica. Così come egli poteva essere affascinato da una patella, noi oggi ricaviamo un provino microscopico da un suo dentino e scopriamo il materiale più resistente in natura. Ispirati dalle giunzioni delle ragnatele, siamo in grado di realizzare le fibre più tenaci al mondo grazie a nodi che scorrendo in trazione dissipano energia per attrito. Osservando il ragno abbiamo scoperto meccanismi con cui questo potrebbe sollevare pesi molto maggiori del suo (idealmente in un paio di mesi anche un uomo di 80 Kg). Leonardo aveva già intuito le leggi che governavano l’attrito, ma certo non poteva investigare su come questo potesse variare a seguito di micro tessiture superficiali, cosa che solo grazie ai calcolatori moderni possiamo progettare e coi laser moderni realizzare. Progettiamo oggi compositi sfruttando singoli fogli atomici come il grafene, prendendo ispirazione dalla struttura della madreperla e replicando l'organizzazione gerarchica di materiali naturali che possiamo attualmente osservare in grande dettaglio grazie a strumenti avanzati di microscopia. Coi cosiddetti “meta-materiali” siamo oggi in grado di controllare la propagazione di onde elastiche, con applicazioni che spaziano dagli scudi sismici ai sistemi per il recupero di energia. Gli esempi potrebbero proseguire, considerando i recentemente scoperti effetti loto di autopulizia o geco di adesione intelligente; il primo è legato alla modifica della bagnabilità di una superficie per effetto della sua rugosità anche gerarchica, che ne aumenta le caratteristiche intrinseche di bagnabilità facendo quindi diventare superfici chimicamente idrofobiche come super-idrofobiche (e sovente autopulenti) come il loto (o viceversa da idrofiliche a super-idrofiliche); il secondo è legato all’incremento di adesione conseguente alla miniaturizzazione dei contatti, essendo la resistenza adesiva proporzionale al perimetro totale degli stessi e non all’area della superficie di contatto. E osservando la natura al microscopio abbiamo scoperto elementi meccanici che si pensava avesse inventato l’uomo, come le stesse ruote dentate. In ultimo, nutrendo i ragni con speciali nanomateriali (nanotubi e grafene), abbiamo verificato come essi siano in grado di produrre una seta rinforzata rispetto alla già resistente e molto tenace controparte naturale, definendo un concetto di composito bionico che supera la stessa ispirazione alla Natura.

La meccanica – scrive Leonardo – è il paradiso delle scienze matematiche perché in quella si viene al frutto**

 

---

[1] G.M. Pugno, Da Dante a Leonardo, sguardo alla storia del pensiero scientifico di due secoli, in «Atti della società degli ingegneri e degli architetti in Torino», 6, 5, 1952, pp. 140-150.

[2] G.M. Pugno, I codici vinciani e la scienza delle costruzioni, «Atti del convegno nazionale per l'istruzione dei geometri e dei periti edili», 1-39 1948; G.M. Pugno, Leonardo da Vinci ed Enrico Betti, https://www.sciencedirect.com/science/article/pii/S2590238519303443 .

[3] G.M. Pugno, Leonardo e le macchine, in «Atti della società degli ingegneri e degli architetti in Torino», 3, 1956, pp. 73-83.

[4] G.M. Pugno, Leonardo da Vinci e l’idraulica. Conferenza Unione Cattolici Artisti Italiani, Sezione di Vercelli, Chieri, G. Astesano, 1956, pp. 8-53.

[5] G.M. Pugno, Da Dante a Leonardo, sviluppo bicentenario del pensiero scientifico, Conferenza tenuta nell'aula magna delle scuole di applicazione d'arma, 1959, pp. 1-28.

[6] I.B. Hart, The mechanical investigations of Leonardo da Vinci, Open Court Publishing Company, Chicago 1925, pp. 1-240. J.H. Randall Jr., The place of Leonardo da Vinci in the emergence of modern science, in «Journal of the History of Ideas», 14, 2, 1953, pp. 191-202. Reti, Leonardo on bearings and gears, in «Scientific American», 224, 2, 1971, pp. 100-111. C. Truesdell, The mechanics of Leonardo da Vinci, in Essays in the History of Mechanics, Springer, Berlin, Heidelberg 1968. R. Pisano, Reflections on the scientific conceptual streams in Leonardo da Vinci and his relationship with Luca Pacioli, in «Advances in Historical Studies», 2, 2, 2013, pp. 32-45. J.P, Byrne, Leonardo da Vinci’s tensile strength tests: implications for the discovery of engineering mechanics, in «Civil Engineering and Environmental Systems», 18, 3, 2001, pp. 243-250. M. Hutchings, Leonardo da Vinci׳s studies of friction, in «Wear», 360-361, 2016, pp. 51-66. K.H. Veltman, Leonardo da Vinci: A Review, in «Leonardo», 41, 4, 2008, pp. 381-388. M.E. Valentinuzzi - G. Pallotti,  Leonardo: The Bioengineer [Retrospectroscope], in «IEEE Pulse», 4, 5, 2013, pp.58-62. D. Lohrmann, U. Alertz, F. Hasters, Teorica and elementi macchinali: two lost treatises of Leonardo da Vinci on mechanics, in «Archives Internationales d’Histoire des Sciences», 62, 168, 2012, pp. 55-84.

[7] A.H. Barber, D. Lu, N.M. Pugno NM (2015) Extreme strength observed in limpet teeth, in «Journal of the Royal Society Interface», 12, 2015 https://royalsocietypublishing.org/doi/full/10.1098/rsif.2014.1326. N.M. Pugno, The “Egg of Columbus” for making the world's toughest fibres, in «PLoS ONE» 9, 4, 2014 www.ing.unitn.it/~pugno/NP_PDF/225-PLOSONE14-knots.pdf. N.M. Pugno, Spider weight dragging and lifting mechanics, in «Meccanica», 53, 2018, pp. 1105-1114. G. Costagliola, F. Bosia, N.M. Pugno, A 2-D model for friction of complex anisotropic surfaces, in «Journal of the mechanics and physics of solids», 112, 2018, pp. 50-65. A.C. Ferrari et al, Science and technology roadmap for graphene, related two-dimensional crystals, and hybrid systems, 2015, www.ing.unitn.it/~pugno/NP_PDF/248-NANOSCALE15-roadmapgraphene.pdf. N.M. Pugno, Mimicking nacres width super-nanotubes for producing optimized super-composites, in «Nanotechnology», 17, 2006, pp. 5480-5484. M. Miniaci, A. Krushynska, F. Bosia, N.M. Pugno, Large scale mechanical metamaterials as seismic shields, in «New journal of physics», 2016, www.ing.unitn.it/~pugno/NP_PDF/300-NJP-metamaterialsseismicshields.pdf . C. Neinhuis, W. Barthlott, Characterisation and distribution of waterrepellent, self-cleaning plant surfaces, in «Ann. Bot», 79, 1997, pp. 667-677. K. Autumn, Y.A. Liang, S.T. Hsieh, W. Zesch, W.P. Chan, T.W. Kenny, R. Fearing, R.J. Full, Adhesive force of a single gecko foot-hair, in «Nature», 405, 2000, pp. 681-685.  E. Arzt, S. Gorb, R. Spolenak, From micro to nano contacts in biological attachment devices, in «Proceeding National Academy of Science», 100, 19, 2003, pp. 10603-10606. M. Burrows, G. Sutton, Interacting gears synchronize propulsive leg movements in a jumping insect, in «Science», 341, 6151,2013, pp. 1254-1256. E. Lepore, F. Bosia, F. Bonaccorso, M. Bruna, S. Taioli, G. Garberoglio, A.C. Ferrari, N.M. Pugno, Spider silk reinforced by graphene or carbon nanotubes, in «2D Materials» 4, 2017, www.ing.unitn.it/~pugno/NP_PDF/300-NJP-metamaterialsseismicshields.pdf.

 

* Questo lavoro rappresenta una traduzione fedele della sua versione in inglese pubblicata dalla rivista «Meccanica» nel numero di dicembre 2019, lanciando la tipologia di articolo “Commemoration”. 

**L’autore ringrazia Massimiliano Fraldi e Federico Bosia per i loro commenti.

 

r/.